Exemplo de Cálculo de Probabilidades Marginais, Conjuntas e Condicionais

Exemplo de Cálculo de Probabilidades Marginais, Conjuntas e Condicionais Através do Método da Freqüência Relativa

Uma empresa quer lançar um produto através de uma campanha de mala direta na PUC. A reitoria envia as cartas sem disponibilizar o seu cadastro de endereços. Ela permite, porém, que a empresa escolha os endereços segundo a ocupação do indivíduo (professor, funcionário ou aluno).

Para examinar a predisposição de cada segmento com relação ao produto, realizou-se uma pesquisa na PUC com 200 entrevistas com pessoas escolhidas ao acaso em hora de grande movimento nos pilotis. Para cada convidado que foi, perguntou-se:

A ocupação do entrevistado : professor, funcionário, aluno
Se gostaria de possuir o produto

O resultado da pesquisa está tabulado abaixo:

	PREDISPOSIÇÃO
Ocupação	POSITIVA	NEGATIVA
Professor	20	10	30
Funcionário	10	10	20
Aluno	70	80	150
	100	100	200

Considere agora o seguinte experimento aleatório:

E1: Envia-se 1 carta para uma pessoa do cadastro escolhida por sorteio.

Neste experimento tem-se dois espaços amostrais,

S1 (profissão) = { professor, funcionário, aluno }

S2 (predisposição) = {+, -}

sendo o espaço amostral resultante o produto carteziano de S1 e S2,

S={(professor, +}, {professor, -},…., (estudante, -) }

Defina agora os seguintes eventos:

A={o indivíduo é professor}

B={ o indivíduo é funcionário }

C={ o indivíduo é aluno }

S: { o indivíduo tem predisposição positiva }

N: { o indivíduo tem predisposição negativa }

Usando o método da freqüência relativa podemos calcular as probabilidades de cada evento simples (probabilidades marginais) e de eventos ocorrendo simultaneamente (probabilidades conjuntas). A tabela abaixo indica a conta a ser feita

	PREDISPOSIÇÃO
Ocupação	POSITIVA	NEGATIVA
Professor	10/200	20/200	30/200
Funcionário	10/200	10/200	20/200
Aluno	80/200	70/200	150/200
	100/200	100/200	200/200

Efetuando os cálculos

	PREDISPOSIÇÃO
Ocupação	POSITIVA	NEGATIVA
Professor	0.05	0.10	0.15
Funcionário	0.05*	0.05	0.1
Aluno	0.40	0.35	0.75**
	0.5**	0.5	1

* Probabilidade Conjunta

**Probabilidade Marginal P(S) e P(C)

A probabilidade de qualquer evento pode ser calculada a partir da tabela acima. Em particular pode-se verificar que:

Probabilidade de ter cartão:

P(S)= 0.5

Probabilidade de ser professor:

P(A)= 0.15

Probabilidade de querer o produto dado que é professor:

P(S/A)= P(A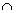

S)/P(A) = 0.05/0.15 = 0.33

Probabilidade de ser funcionário

P(B)= 0.75

Probabilidade de querer o produto dado que é funcionário:

P(S/B) = P(B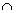

S)/P(B)= 0.05/0.1=0.5

Probabilidade de querer o produto dado que é estudante:

P(S/C) = P(C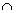

S)/P(C)= 0.35/0.75=0.47

Note que como P(S/B) = P(S) os eventos T e B são independentes

Informações importantes para a tomada de decisão podem ser extraídas dos cálculos acima. Algumas delas estão listadas abaixo

Os funcionários é que apresentam o maior índice de aceitação do produto. Porém, a probabilidade da carta chegar a um destinatário que quer o produto é independente do fato de ser funcionário. Portanto, tanto faz mandar a carta para uma destinatário sorteado dentre os funcionários ou mandar para um sorteado do cadastro completo. Isto acontece porque B e S são eventos independentes.

A situação muda se o número de cartas a ser enviado for maior e for possível escolher a classe de ocupação dentro da qual serão sorteados os endereços. Por exemplo, se existem 10000 nomes no cadastro e o número de cartas é de 2000, a melhor política é enviar para todos os funcionários (que formam, segundo a pesquisa cerca de 1/10 do cadastro) e depois sortear os endereços restantes dentre os alunos.

Exemplo de Utilização da Regra de Bayes em "Credit Score"

Exemplo de Aplicação da Regra de Bayes em Marketing