Neste exemplo, com os critérios do mínimo erro médio quadrático e do mínimo erro absoluto, são calculados os coeficientes de um equalizador de 3 derivações para equalização de um sinal PAM cujo pulso básico é dado na Figura 23, após passar por um filtro de recepção passa-baixa ideal de faixa igual a 1/2T. É feita também ao longo do exemplo uma comparação de desempenho dos equalizadores em presença de IES e ruído.

Para o critério do erro médio quadrático os coeficientes devem ser calculados através da equação (79), o que exige o conhecimento da função autocorrelação R_y(kT). Pode-se mostrar que

onde s _a² e s _n² são, respectivamente, as variâncias da amplitude transmitida e da amostra do ruído no detetor e d _i é definido na equação (89).

Solução sem ruído

Supondo s _a² = 1 e desprezando inicialmente o ruído tem-se

Para i = 1 tem-se o seguinte desenvolvimento :

Fazendo o mesmo para i = - 1 e i = 0 chega-se à matriz

cuja inversa é

Notando que

chega-se a

W_-1 = -0,18 W_o = 1,107 W₁ = -0,432

Na saída do equalizador tem-se a seguinte expressão para as amostras do novo pulso básico p(t) :

Com os coeficientes calculados anteriormente tem-se os seguintes valores:

p(-2T) = -0,036; p(-T) = 0,414; p(0) = 0,931; p(T) = 0,1215; p(2T) = -0,216.

Embora o valor médio quadrático do erro possa ser calculado através da equação (82), neste caso é mais simples calculá-lo a partir das amostras do pulso equalizado. Pode-se mostrar que o erro médio quadrático é dado pela soma dos quadrados das amostras para k¹ 0 mais o quadrado da diferença entre a amostra desejada (1) e a amostra p(0). Chega-se então a e = 0,069. Para o valor máximo da interferência entre símbolos tem-se,

Note-se que, antes do equalizador, o erro médio quadrático e o valor máximo da interferência entre símbolos são iguais a 0,29 e 0,7, respectivamente.

Com o critério do erro absoluto os coeficientes devem ser calculados através da equação (93). Tem-se então,

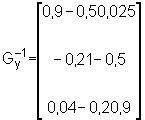
W_-1 = -0,25 W_o = 1,25 W₁ = -0,625

p(-2T) = -0,05; p(-T) = p(T) = 0; p(2T) = -0,312; p(0) = 1

e = 0,1 z_max = 0,362

Note-se, portanto, que ambos os equalizadores reduzem drasticamente o erro médio quadrático e o valor máximo da interferência entre símbolos. Porém, como era esperado, o primeiro equalizador leva a um menor erro médio quadrático e a um maior valor máximo da interferência entre símbolos em relação ao segundo equalizador.

Solução com ruído

Considerando agora na entrada do equalizador um ruído de variância igual a

chega-se, no caso do critério do erro médio quadrático, aos seguintes resultados

p(-2T) = -0,016; p(-T) = 0,103; p(0) = 0,807 p(T) = 0,145; p(2T) = 0,156

Para calcular a variância do ruído na saída do equalizador deve-se notar que, na saída do filtro de recepção o ruído n'(t) tem a seguinte densidade espectral de potência

A potência de ruído n''(t) na saída do equalizador será dada então por

Notando que

chega-se a

Usando nesta expressão os conjuntos de coeficientes calculados anteriormente e lembrando que N_o/2T = 0,1, obtém-se s _n,², = 0,202, s _n,², = 0,144 e s _n,², = 0,093 para os equalizadores EMQ, ZF e EMQ em presença de ruído, respectivamente.

Para uma comparação geral de desempenho, os resultados obtidos podem ser grupados na Tabela 1
 

Nota-se que os dois primeiros equalizadores, por não considerarem o ruído, levam a um aumento da potência de ruído na saída. Isto deverá acontecer sempre com o equalizador ZF teórico, cujo critério de otimização é baseado exclusivamente na interferência entre símbolos. Na prática, entretanto, como se verá a seguir, os equalizadores são implementados através de algoritmos iterativos, onde a influência do ruído estará presente, em geral em todas as formas de equalização.