Diagonalização e Forma Canônica de Jordan

A forma diagonal de uma matriz

Seja uma matriz A n por n que tenha autovetores linearmente independentes. Se estes vetores forem escolhidos para serem as colunas de uma matriz S, tem-se que S-1AS é a matriz diagonal L, com os autovetores de A em sua diagonal principal.
 

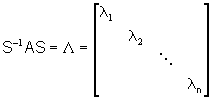
Obs: Chamamos S de "matriz dos autovetores" e L de "matriz de autovalores".

Podemos tirar as seguintes relações:

AS = SL, ou S-1AS = L, ou A = SLS-1

A matriz S é inversível, porque assumimos que suas colunas (os autovetores) são linearmente independentes.

Exemplo

Forma Canônica de Jordan

A forma de Jordan tem como objetivo tornar a matriz M-1AM mais diagonal possível. Se os autovetores de uma matriz A forem linearmente independentes, então M = S e chegamos à J = S-1AS = L; a forma de Jordan coincide com a matriz diagonal L. Isto é impossível para uma matriz defectiva, e para cada autovetor que faltar a matriz de Jordan terá um 1 acima de sua diagonal principal. Os autovalores aparecem na própria diagonal, porque J é triangular. E autovalores distintos podem sempre ser desacoplados. Ou seja, só l repetidos que ocasionarão elementos fora da diagonal principal em J.
Se A possuir s autovetores independentes, é similar à uma matriz com s blocos:
 
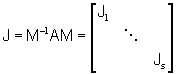
Cada bloco Ji é uma matriz triangular com somente um autovalor li e um autovetor:
 

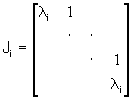
Quando o bloco tiver uma ordem m > 1, o autovalor lié repetido m vezes e existirão 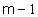1's acima da diagonal. O mesmo autovalor li deverá aparecer em alguns blocos, se este corresponder a vários autovetores independentes. Duas matrizes são similares se elas tiverem a mesma forma de Jordan J.

Exemplo