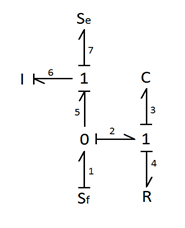
Realizando el desarrollo por el método de grafos de conexión, para variables de potencia:
 S_e
S_e - Fuente de esfuerzo
S_f - Fuente de flujo
I - Inercia de la masa
C - Capacitores que modelan el muelle
R - Resistencias que modelan el amortiguador
Ecuaciones:
\begin{matrix}
\varrho_{5} = \varrho_{2} & f_{3} = f_{2} & f_{7} = f_{6}\\
\varrho_{5} = \varrho_{2} & f_{4} = f_{2} & f_{5} = f_{6} \\
f_{5} = f_{1} - f_{5} & \varrho_{2} = \varrho_{3} + \varrho_{4} & \varrho_{6} = \varrho_{5} - \varrho_{7}\\
\end{matrix}
Realizados los desarrollos necesarios, la forma matricial final:
\begin{bmatrix}
\dot{f_{6}} \\
\dot{\varrho_{3}}
\end{bmatrix} = \begin{bmatrix}
- \frac{b}{m}& \frac{1}{n} \\
- \frac{1}{k} & 0 \\
\end{bmatrix} . \begin{bmatrix}
f_{6} \\
\varrho_{3}
\end{bmatrix} + \begin{bmatrix}
\frac{b}{m}& \frac{1}{n} \\
\frac{1}{k} & 0 \\
\end{bmatrix} . \begin{bmatrix}
f_{1} \\
\varrho_{7}
\end{bmatrix} \\
~~~~~\begin{bmatrix}
f_{1} \\
\varrho_{7}
\end{bmatrix} = \begin{bmatrix}
1 & 0 \\
-b & 1 \\
\end{bmatrix} . \begin{bmatrix}
f_{6} \\
\varrho_{3}
\end{bmatrix} + \begin{bmatrix}
0 & 0 \\
b& 0 \\
\end{bmatrix}.\begin{bmatrix}
f_{1} \\
\varrho_{7}
\end{bmatrix}
Parámetros de sistema:
