Otra forma de controlar el sistema es a través de la realimentación de estados, que consiste en realimentar todos los estados del sistema, multiplicados por una matriz de ganancia K en vez de usar la salida del sistema como realimentación. Esto permite reposicionar los polos del sistema para alterar sus características.
La imagen siguiente representa el diagrama de bloques de la planta original con el control pro realimentación de estados.
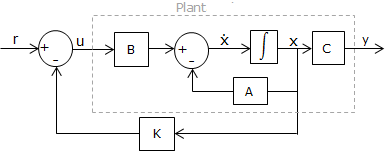
Como visto anteriormente, dados los parámetros del sistema del motor DC:
El espacio de estados del sistema sin control se vuelve:
La posición inicial de los polos son los valores propios de la matriz A. Los mismos pueden ser verificados:
A través de realimentación, es posible obtener un nuevo sistema en que los polos de la malla cerrada pueden ser reposicionados arbitrariamente si el par (A, B) es controlable.
El sistema es controlable cuando posición de la matriz A_{nxn} es igual a n, en este caso, n necesita ser igual a 2.
Después de verificar la controlabilidad, podemos determinar la nueva posición deseada para los polos:
Y así, a través de la fórmula de Ackerman, calcular el valor de K, que realiza el ajuste necesario:
Finalmente, podemos aplicar la ganancia K en la malla de realimentación y llegar al sistema controlado. El sistema original presentaba la forma:
\dot{x}=Ax+Bu
y=Cx
El sistema controlado tendrá la forma:
\dot{x}=\left ( A-Bk \right )x+Bu
y=Cx
Así, podemos verificar la nueva posición de los polos del Sistema realimentado a través de los valores propios de (A-B.k):
|

