Conforme apresentado anteriormente, foi definido que as saídas do sistema são as correntes no circuito do receptor, ou seja:
y_{1}(t)\overset{\underset{\mathrm{def}}{}}{=}i_{R}(t)
y_{2}(t)\overset{\underset{\mathrm{def}}{}}{=}i_{a}(t)
Analisando a Matriz de Transferência, pode-se a determinar a Transformada de Laplace do Vetor de Saída:
\underline {\underline{Y}}(s)=\begin{bmatrix}
I_{r}(s)\\
I_{a}(s)\\
\end{bmatrix}=\begin{bmatrix}
Y_{1}(s)\\
Y_{2}(s)\\
\end{bmatrix}=\begin{bmatrix}
H_{11}(s)&&H_{12}(s)\\
H_{21}(s)&&H_{22}(s)\\
\end{bmatrix}
\begin{bmatrix}
V_1(s)\\
V_2(s)\\
\end{bmatrix}
Percebe-se, pois, que cada uma das Funções de Transferência contribui com uma parcela das saídas.
Os simuladores a seguir apresentam as respostas ao degrau unitário aplicado em ambas as entradas,
V_{1}(s) e
V_{2}(s) . Os dois diagramas em blocos a seguir representam o sistema quando Controladores PID não utilizados em cada relação entrada-saída.
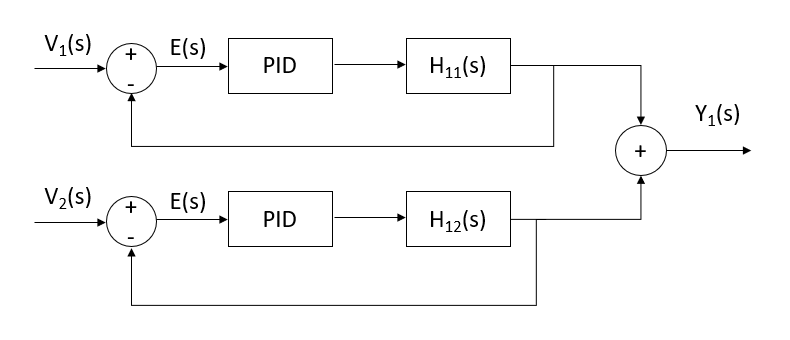
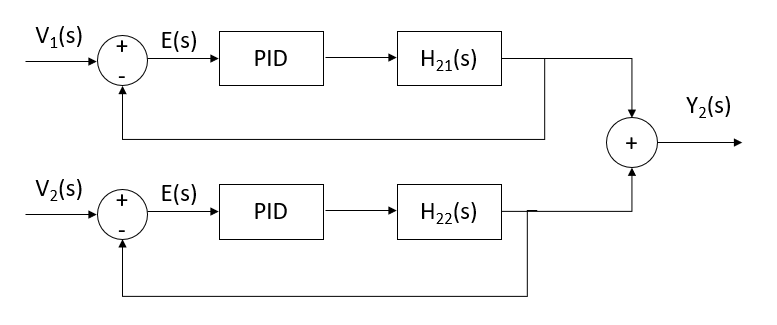
Determine, a seguir, a resposta completa da saída
y_{1}(t)\overset{\underset{\mathrm{def}}{}}{=}i_{R}(t) devida aos degraus unitários aplicados em cada uma das entradas.
OBS: Para cada entrada, foi definido um conjunto de ganhos PID.

