Controlável e não observável

2) É possível achar um conjunto de b_ij e um de c_ij tal que a equação abaixo seja controlável? Observável?

Pode ser observável
Não pode se controlável

3) Para a equação abaixo, é possível escolher um estado em t=0 tal que a saída seja da forma  para t>0 ?

Solução (matemática):

Analogamente a equações diferenciais o termo te^-t deve-se à raiz repetida

Se 

a solução poderia ser simplesmente:
Como a equação é observável, todos os modos  aparecem na saída y(t). Portanto, uma escolha adequada de x(0) faz com que só um dos modos (te ^t neste caso) permaneça.
 

4) Encontre a equação dinâmica que descreve o diagrama de blocos abaixo:

 

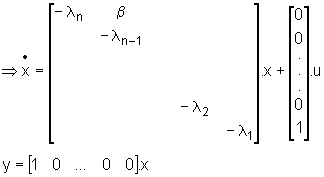
Obs:  , que pode ser facilmente "realizada" na forma companheira, por exemplo.
 
 

5) Transforme a equação abaixo para a forma controlável:

Pode-se resolver este problema de inúmeras formas:

1° ) Achando a função de tranferência diretamente da equação dinâmica:

Identificando os a_i e b _i ,basta colocar na forma controlável
 

2° ) Obtendo G(s) a partir do diagrama de blocos:

3° ) Através de uma transformação de equivalência
(demonstração em: Introduction to Linear Theory-C.T.Chen):

cujas colunas formam a nova base.
  ,onde  é a matriz de controlabilidade da equação na forma canônica controlável.
Os a_i podem ser obtidos do polinômio característico da matriz A dada.

Portanto, neste exemplo:

A matriz  só depende dos a_I já calculados.
O vetor  é sempre da mesma forma.
Logo, necessitamos Q somente para obter o vetor :

A forma canônica controlável é:

Obs:

1)No caso de se desejar obter a forma canônica onservável, o procedimento é semelhante. Neste caso, o vetor  tem que ser calculado.Sabe-se que =Pb;

P é dado por:
, onde V e  são as matrizes de observabilidade da equação dada e da equação na forma observável, respectivamente.

vista no exercício 5.

2) Se a equação dinâmica original for controlável e observável, basta achar uma das formas canônicas e "transpor"as matrizes para obter a outra forma canônica.