Cálculo Numérico Aproximado de Integrais:

a) Aproximação por retângulos, como na definição;

b) Regra dos Trapézios:

     
Área do trapézio aproximante que passa por: (0, f0) , (h, f1)

Para n intervalos:


 
 
Teorema: Suponha f(.) duas vezes continuamente diferenciável em [a, b]. Então:

,

para algum , a < < b
Conclusão: Se f(.) é limitada em (a, b), a aproximação converge para  quando (isto é, ), pois

,

"quadraticamente" em h;

c) Regra de Simpson:
 


 

Área sobre a parábola aproximante que passa por: (0, f0), (h, f1), (2h, f2)

Para n=2m


 
Teorema: Suponha f(.) quatro vezes continuamente diferenciável em [a, b]. Então:

, para algum , a < < b

Conclusão: Se f(4)(.) é limitada em [a, b], a aproximação converge para  quando  (isto é, ), pois  e 

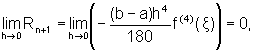
com "ordem 4" em h.

Nota: Existe a regra para um número ímpar de intervalos.

Exemplo:


 
m Regra dos 
trapézios
h Regra de Simpson h
3 0.03846 0.02564 1
5 0.05371 0.4 0.05880 0.5
7 0.05689 0.2857 0.05424
9 0.05772 0.05906 0.25
11 0.05795 0.1818 0.05721 0.2
13 0.05801 0.1538 0.05839

Valor exato: 0.0580256