Detalhes sobre a Modelagem do Sistema

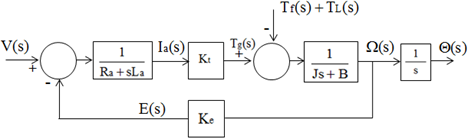
A equação elétrica pode ser obtida a partir da Lei de Kirchhoff no circuito de armadura. A partir das Leis de Newton para o movimento rotacional, pode-se determinar as equações mecânicas. E, finalmente, a relação entre a parte elétrica e a mecânica é obtida pela Lei de Faraday-Neumann-Lenz.

Aplicando a Transformada de Laplace, obtêm-se as equações no domínio da frequência:

V\left ( s \right )=R_{a}\cdot I_{a}+s\cdot L_{a}\cdot I_{a}+E\left ( s \right )
T_{g}\left ( s \right )=J\cdot s\cdot \Omega \left ( s \right )+B\cdot \Omega \left ( s \right )+T_{s}\left ( s \right )+T_{L}\left ( s \right )
T_{g}=K_{t}\cdot I_{a}\left ( s \right )
E\left ( s \right )=K_{e}\cdot \Omega \left ( s \right )

Onde:

J - Inércia total do rotor e da carga em relação ao eixo.
B - Constante de atrito viscoso.
T_{f} - Torque referente ao atrito na carga e no motor (é parte do conjugado de perdas Tw).
K_{t} - Constante de torque do motor.
K_{e} - Constante da força eletromotriz.

Note que K_{t}=K_{e}, pois a potência mecânica desenvolvida deve ser igual a potência elétrica absorvida no rotor.

Estas equações podem ser representadas pelo seguinte diagrama de blocos: