DEPARTAMENTO DE MATEMÁTICA PUC-RIO
CICLO BÁSICO DO CTC.
P1- CALCULO I (29-09-98)
-
1) (JUSTIFIQUE SUAS RESPOSTAS) Decida se cada proposição
abaixo é falsa ou verdadeira.
-
-
a) Se
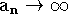 e
e 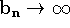 então
então 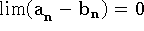 .
.
-
Solução: Falso.
-
Contra-exemplo:
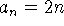 e
e 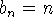 .
.
-
Observe que
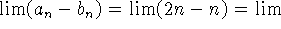
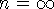
-
b) Se
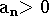 e
e 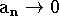 então
então 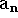 é uma sequência decrescente.
é uma sequência decrescente.
-
Solução: Falso,
-
como contra-exemplo considere a seguinte sequência:

-
c) Se
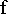 é uma função real definida por
é uma função real definida por 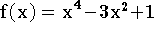 então
então 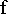 possui no mínimo uma raiz no intervalo
possui no mínimo uma raiz no intervalo 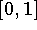 .
.
-
Solução: Verdadeiro.
-
Desde que
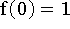 e
e 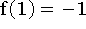 , a função
, a função 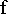 é contínua (Polinômio) e
é contínua (Polinômio) e 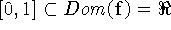 então pelo teorema do valor intermediário, para qualquer
então pelo teorema do valor intermediário, para qualquer 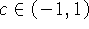 temos que existe
temos que existe 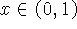 tal que f(x) = c. Em particular, como
tal que f(x) = c. Em particular, como 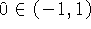 então f(x) = 0 para algum
então f(x) = 0 para algum 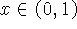 .
.
-
2) (JUSTIFIQUE SUAS RESPOSTAS) Decida se as sequências dadas abaixo
convergem e em caso afirmativo determine o limite:
-
a)
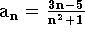
-
Solução:
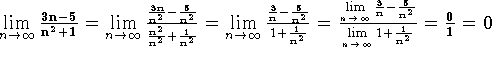
-
b)
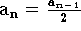 com
com 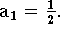
-
Solução:
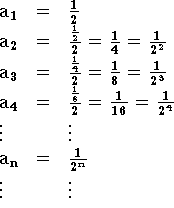
Observe que 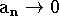 pois
pois 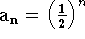 e toda sequência da forma
e toda sequência da forma 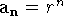 com 0<r<1 converge para zero. (Teorema visto em sala de aula).
com 0<r<1 converge para zero. (Teorema visto em sala de aula).
-
3) Considere
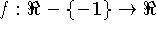 uma função com as seguintes propriedades:
uma função com as seguintes propriedades:
-
a) f é contínua.
-
b) f é crescente no intervalo
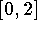 .
.
-
c) f é decrescente nos intervalos
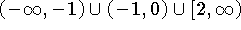 .
.
-
d)
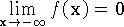 ,
, 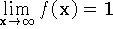 ,
, 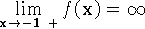 ,
, 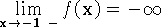 ,
, 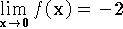
-
-
Solução:
-
-
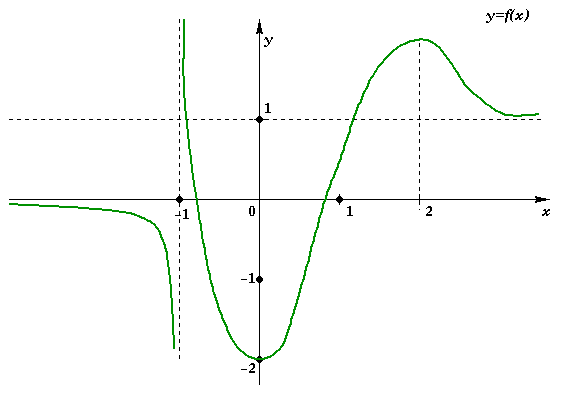
4) (JUSTIFIQUE SUAS RESPOSTAS) Considere uma função
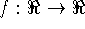 cujo gráfico é dado pela figura abaixo:
cujo gráfico é dado pela figura abaixo:
-
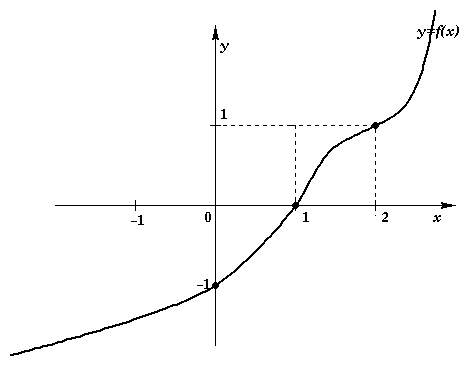
-
a) Desenhe o gráfico da função
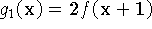
-
Solução:
-
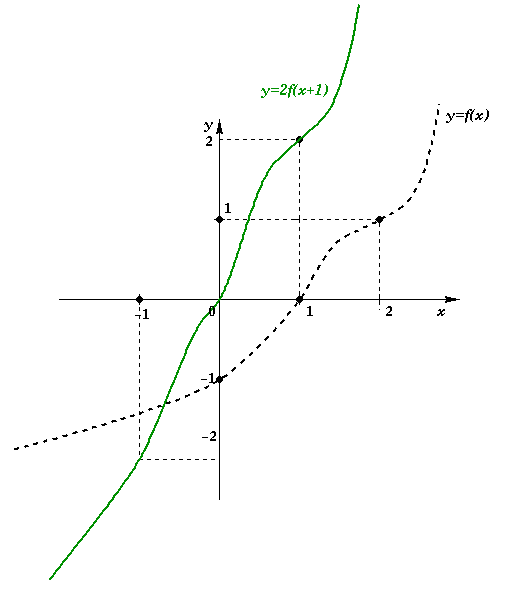
Observe que 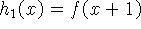 é uma translação horizontal a esquerda de uma unidade
e
é uma translação horizontal a esquerda de uma unidade
e 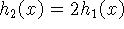 é uma expansão vertical uniforme.
é uma expansão vertical uniforme.
-
b) Desenhe o gráfico da função inversa
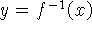
-
Solução:
-
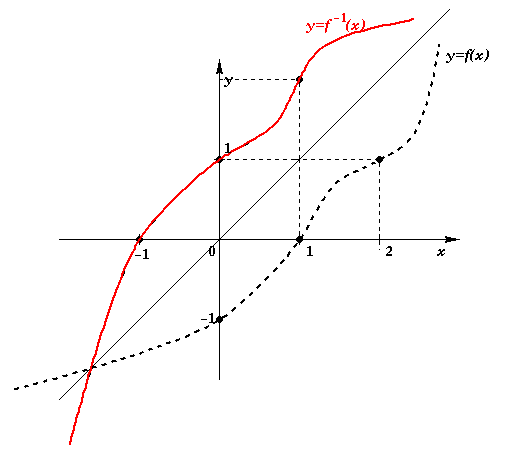
O gráfico da função inversa é obtido através
de uma reflexão em torno da reta y = x.
-
5)
-
a) (JUSTIFIQUE SUAS RESPOSTAS) Considere a função
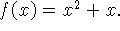
-
i) Utilize a definição de derivada para determinar a expressão
de
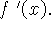
-
Solução:
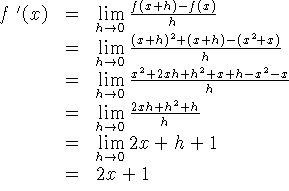
-
ii) Determine a equação de uma reta que seja tangente
ao gráfico de
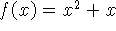 e que passe pelo ponto P(2,5). (Se houver mais de uma,
escolha uma delas).
e que passe pelo ponto P(2,5). (Se houver mais de uma,
escolha uma delas).
-
Solução: Observe que o ponto P(2,5) não pertence
ao gráfico da função. Assim é necessário
determinar o ponto de tangência da reta com o gráfico. Considere
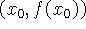 o ponto em que a reta que passa pelo ponto P(2,5) tangencia o gráfico
da função. Assim o coeficiente angular desta reta será
o ponto em que a reta que passa pelo ponto P(2,5) tangencia o gráfico
da função. Assim o coeficiente angular desta reta será 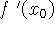 e portando a equação da reta será:
e portando a equação da reta será:
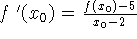
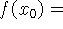
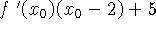
-
No ponto
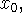 temos que
temos que 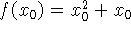 a derivada é
a derivada é 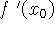
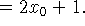 Substituindo na equação da reta:
Substituindo na equação da reta:
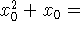
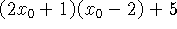
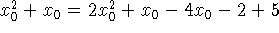
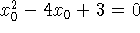
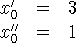
-
Assim temos dois pontos de tangência e portanto duas retas possíveis.
-
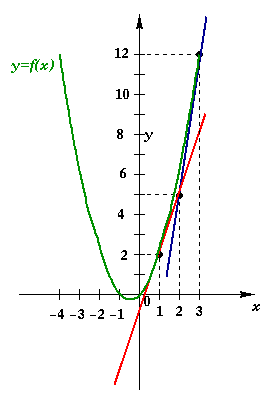
-
i) Para
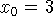 temos f(3)=9+3 =12 e
temos f(3)=9+3 =12 e 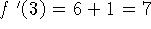 e portanto a equação da reta será:
e portanto a equação da reta será:
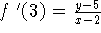
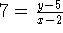 y = 7(x-2)+5
y = 7x-9
y = 7(x-2)+5
y = 7x-9
-
ii) Para
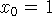 temos f(1) = 1+1 = 2 e
temos f(1) = 1+1 = 2 e 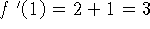 e portanto a equação da reta será:
e portanto a equação da reta será:
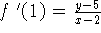
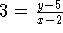 y = 3(x-2)+5
y = 3x-1
y = 3(x-2)+5
y = 3x-1
-
b) Os gráficos abaixo podem ser agrupados em pares tais que cada
par é composto pelo gráfico de uma função e
o gráfico de sua derivada. Identifique os pares explicitando qual
é o gráfico da função e qual é o gráfico
da derivada.
Solução:
pois
e toda sequência da forma
com 0<r<1 converge para zero. (Teorema visto em sala de aula).