Considere-se o circuito:
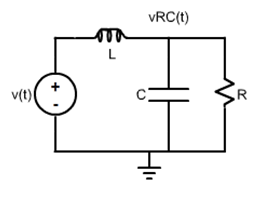
O circuito será estudado utilizando duas possíveis saídas: (1) a tensão no indutor; e (2) a tensão no circuito paralelo
RC, designada no diagrama
V_{RC}(t).
As funções de transferência para cada uma das saídas são:
H_{L}(s) = \frac{s^2 + \frac{1}{RC} s}{s^2 + \frac{1}{RC} s + \frac{1}{LC}}
H_{RC}(s) = \frac{\frac{1}{LC}}{s^2 + \frac{1}{RC} s + \frac{1}{LC}}
As Transformadas de Laplace das saídas, devidas a uma entrada genérica
v(t), cuja Transformada de Laplace é
V(s), são:
V_{L}(s) = H_{L}(s) V(s) = \frac{s^2 + \frac{1}{RC} s}{s^2 + \frac{1}{RC} s + \frac{1}{LC}} V(s)
V_{RC}(s) = H_{RC}(s) V(s) = \frac{\frac{1}{LC}}{s^2 + \frac{1}{RC} s + \frac{1}{LC}} V(s)
As respectivas funções de saída no tempo podem ser determinadas através das expressões:
V_{L}(t) = \mathcal{L} \begin{bmatrix} \frac{s^2 + \frac{1}{RC} s}{s^2 + \frac{1}{RC} s + \frac{1}{LC}} V(s) \end{bmatrix}
V_{RC}(t) =\mathcal{L} \begin{bmatrix} \frac{\frac{1}{LC}}{s^2 + \frac{1}{RC} s + \frac{1}{LC}} V(s) \end{bmatrix}
A seguir, compute as respostas às funções escolhidas. Para cada uma das funções, defina os parâmetros a serem usados escrevendo-os nas “caixas”.
• Respostas no Domínio do Tempo
Resposta Impulsional da Tensão no Indutor
• Respostas no Domínio da Frequência – Diagrama de Bode
O Diagrama de Bode, com seus gráficos de módulo e fase, é determinado a seguir. Para tal, escolha os valores dos parâmetros e a faixa de frequências.
Diagrama de Bode da Tensão no Indutor

